5854. Максимальная сумма базовая
Дана прямоугольная таблица
размером n строк на m столбцов. В каждой клетке этой таблицы
записано целое число. По таблице можно пройти сверху вниз, начиная с любой
клетки верхней строки, и на каждом шаге перемещаться в одну из “нижних соседних”
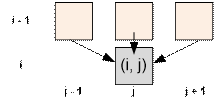
клеток. Иными словами, из клетки с координатами (i, j) можно перейти в
(i + 1, j – 1), (i + 1, j)
или (i + 1, j + 1). Если j = m, последний из трёх вариантов перехода невозможен. Если j = 1, невозможен первый
вариант. Маршрут заканчивается в одной из клеток нижней строки.
Напишите программу, которая
находит максимальную сумму значений пройденных клеток среди всех допустимых
путей.
Вход. В
первой строке заданы n и m (1 ≤ n, m ≤ 200) – количество строк и столбцов. Далее в
каждой из следующих n строк
записано по m целых чисел (не
превышающих по модулю 106) – значения клеток таблицы.
Выход. Выведите
единственное число – найденную максимальную сумму.
|
Пример
входа |
Пример
выхода |
|
4 3 1 15 2 9 7 5 9 2 4 6 9 -1 |
42 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть a[i][j] – исходная
таблица. Обозначим через dp[i][j] максимальную сумму чисел на пути от любой клетки первой
строки до клетки (i, j). Тогда
dp[i][j] = max(dp[i – 1][j – 1], dp[i – 1][j], dp[i – 1][j + 1]) + a[i][j]
Для корректного
вычисления значений в первом и последнем столбцах положим
dp[i][0] = dp[i][m + 1] = -∞
Инициализируем первую
строку массива dp значениями первой строки таблицы а:
dp[1][i] = a[1][i], 1
≤ i ≤ m
Ответом на
задачу будет максимальное значение в последней (n-ой) строке массива
dp.
Пример
Рассмотрим
входной тест.
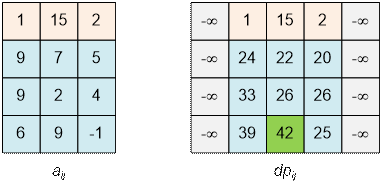
Реализация алгоритма
Объявим
константу MIN для хранения минимального
значения, а также массивы a и dp.
#define MAX 202
#define MIN
-2000000000
int a[MAX][MAX], dp[MAX][MAX];
Читаем
входные данные. Верхний левый угол таблицы будем хранить в a[1][1]. Столбцы
с номерами 0 и m + 1 в массиве dp заполним
минимально возможным значением MIN.
scanf("%d %d",
&n, &m);
for (i = 1; i <= n; i++)
{
dp[i][0]
= dp[i][m + 1] = MIN;
for (j =
1; j <= m; j++)
scanf("%d",
&a[i][j]);
}
Скопируем
первую строку массива а в массив dp.
for (i = 1; i <= n; i++)
dp[1][i] =
a[1][i];
Пересчитаем
максимальные суммы на путях от верхней строки до клетки (i, j) и сохраним их в массиве dp.
for (i = 2; i <= n; i++)
for (j = 1; j <= m; j++)
dp[i][j] = max(max(dp[i -
1][j - 1], dp[i - 1][j]),
dp[i - 1][j + 1]) + a[i][j];
Найдем
наибольшее число в последней (n-ой) строке массива dp.
res = MIN;
for (i = 1; i <= m; i++)
if (dp[n][i]
> res) res = dp[n][i];
Выводим
ответ.
printf("%d\n",
res);
Java реализация
import java.util.*;
public class Main
{
static int a[][], dp[][];
final static int MIN = -2000000000;
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
dp = new int[n+1][m+2];
a = new int[n+1][m+2];
for (int i = 1; i <= n; i++)
{
dp[i][0] = dp[i][m + 1] = MIN;
for (int j = 1; j <= m; j++)
a[i][j] = con.nextInt();;
}
for (int i = 1; i <= m; i++)
dp[1][i] = a[1][i];
for (int i = 2; i <= n; i++)
for (int j = 1; j <= m; j++)
dp[i][j] = Math.max(Math.max(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + a[i][j];
int res = MIN;
for (int i = 1; i <= m; i++)
if (dp[n][i] > res) res = dp[n][i];
System.out.println(res);
con.close();
}
}